Portal:Mathematics

The Mathematics Portal

Emmy Noether

Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Featured articles –

  Featured articles are displayed here, which represent some of the best content on English Wikipedia.

---

• 
  In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.
  
  Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...)
• 

  

  Plots of logarithm functions, with three commonly used bases. The special points log_b b = 1 are indicated by dotted lines, and all curves intersect in log_b 1 = 0.

  
  
  In mathematics, the logarithm to base b is the inverse function of exponentiation with base b. That means that the logarithm of a number x to the base b is the exponent to which b must be raised to produce x. For example, since 1000 = 10³, the logarithm base $10$ of 1000 is 3, or log₁₀ (1000) = 3. The logarithm of x to base b is denoted as log_b (x), or without parentheses, log_b x. When the base is clear from the context or is irrelevant it is sometimes written log x.
  
  The logarithm base 10 is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number e ≈ 2.718 as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base 2 and is frequently used in computer science. (Full article...)
• 

  

  Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.

  
  
  In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).
  
  In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...)
• 

  

  The weighing pans of this balance scale contain zero objects, divided into two equal groups.

  
  In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—indeed, 0 + x and x always have the same parity.
  
  Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
• 
  
  

  

  Rejewski, c. 1932

  
  Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ^ⓘ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.
  
  Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
• 
  
  

  

  Bust of Shen at the Beijing Ancient Observatory

  
  Shen Kuo (Chinese: 沈括; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁), was a Chinese polymath, scientist, and statesman of the Song dynasty (960–1279). Shen was a master in many fields of study including mathematics, optics, and horology. In his career as a civil servant, he became a finance minister, governmental state inspector, head official for the Bureau of Astronomy in the Song court, Assistant Minister of Imperial Hospitality, and also served as an academic chancellor. At court his political allegiance was to the Reformist faction known as the New Policies Group, headed by Chancellor Wang Anshi (1021–1085).
  
  In his Dream Pool Essays or Dream Torrent Essays (夢溪筆談; Mengxi Bitan) of 1088, Shen was the first to describe the magnetic needle compass, which would be used for navigation (first described in Europe by Alexander Neckam in 1187). Shen discovered the concept of true north in terms of magnetic declination towards the north pole, with experimentation of suspended magnetic needles and "the improved meridian determined by Shen's [astronomical] measurement of the distance between the pole star and true north". This was the decisive step in human history to make compasses more useful for navigation, and may have been a concept unknown in Europe for another four hundred years (evidence of German sundials made circa 1450 show markings similar to Chinese geomancers' compasses in regard to declination). (Full article...)
• 
  
  

  

  Noether c. 1900–1910

  
  Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She proved Noether's first and second theorems, which are fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.
  
  Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
• 

  

  
  Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is best known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.
  
  Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)
• 

  

  The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group S̃₃

  
  The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers (..., −2, −1, 0, 1, 2, ...) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.
  
  A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)
• 
  
  

  

  Portrait by August Köhler, c. 1910, after 1627 original

  
  Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ^ⓘ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.
  
  Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
  Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. (Full article...)
• 
  In classical mechanics, the Laplace–Runge–Lenz (LRL) vector is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.
  
  The hydrogen atom is a Kepler problem, since it comprises two charged particles interacting by Coulomb's law of electrostatics, another inverse-square central force. The LRL vector was essential in the first quantum mechanical derivation of the spectrum of the hydrogen atom, before the development of the Schrödinger equation. However, this approach is rarely used today. (Full article...)
• 
  
  

  

  Hilary Putnam

  
  The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.
  
  Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)
• 
  
  

  

  Kaczynski after his arrest in 1996

  
  Theodore John Kaczynski (/kəˈzɪnski/ ^ⓘ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ ^ⓘ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle.
  
  Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored Industrial Society and Its Future, a 35,000-word manifesto and social critique opposing all forms of technology, rejecting leftism, and advocating a nature-centered form of anarchism. (Full article...)
• 
  
  

  

  Elementary algebra studies which values solve equations formed using arithmetical operations.

  
  Algebra is the branch of mathematics that studies certain abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.
  
  Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
• 
  General relativity, also known as the general theory of relativity, and as Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time, or four-dimensional spacetime. In particular, the curvature of spacetime is directly related to the energy and momentum of whatever present matter and radiation. The relation is specified by the Einstein field equations, a system of second-order partial differential equations.
  
  Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitation in classical physics. These predictions concern the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light, and include gravitational time dilation, gravitational lensing, the gravitational redshift of light, the Shapiro time delay and singularities/black holes. So far, all tests of general relativity have been shown to be in agreement with the theory. The time-dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for cosmology, thus leading to the discovery of the Big Bang and cosmic microwave background radiation. Despite the introduction of a number of alternative theories, general relativity continues to be the simplest theory consistent with experimental data. (Full article...)

Selected image –

animation showing a right triangle being duplicated and rearranged in a way that illustrates the Pythagorean theorem

Pythagorean theorem

Credit: User:Alvesgaspar

An animated geometric proof of the Pythagorean theorem, which states that among the three sides of a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides, written as a² + b² = c². A large square is formed with area c², from four identical right triangles with sides a, b and c, fitted around a small central square (of side length b − a). Then two rectangles are formed with sides a and b by moving the triangles. Combining the smaller square with these rectangles produces two squares of areas a² and b², which together must have the same area as the initial large square. This is a somewhat subtle example of a proof without words.

Good articles –

  These are Good articles, which meet a core set of high editorial standards.

---

• 

  

  A graph with a universal vertex, u

  
  In graph theory, a universal vertex is a vertex of an undirected graph that is adjacent to all other vertices of the graph. It may also be called a dominating vertex, as it forms a one-element dominating set in the graph. A graph that contains a universal vertex may be called a cone, and its universal vertex may be called the apex of the cone. This terminology should be distinguished from the unrelated usage of these words for universal quantifiers in the logic of graphs, and for apex graphs.
  
  Graphs that contain a universal vertex include the stars, trivially perfect graphs, and friendship graphs. For wheel graphs (the graphs of pyramids), and graphs of higher-dimensional pyramidal polytopes, the vertex at the apex of the pyramid is universal. When a graph contains a universal vertex, it is a cop-win graph, and almost all cop-win graphs contain a universal vertex. (Full article...)
• 
  Advanced Placement (AP) Statistics (also known as AP Stats) is a college-level high school statistics course offered in the United States through the College Board's Advanced Placement program. This course is equivalent to a one semester, non-calculus-based introductory college statistics course and is normally offered to sophomores, juniors and seniors in high school.
  
  One of the College Board's more recent additions, the AP Statistics exam was first administered in May 1996 to supplement the AP program's math offerings, which had previously consisted of only AP Calculus AB and BC. In the United States, enrollment in AP Statistics classes has increased at a higher rate than in any other AP class. (Full article...)
• 
  
  

  

  Bernt Michael Holmboe

  
  Bernt Michael Holmboe (23 March 1795 – 28 March 1850) was a Norwegian mathematician. He was home-tutored from an early age, and was not enrolled in school until 1810. Following a short period at the Royal Frederick University, which included a stint as assistant to Christopher Hansteen, Holmboe was hired as a mathematics teacher at the Christiania Cathedral School in 1818, where he met the future renowned mathematician Niels Henrik Abel. Holmboe's lasting impact on mathematics worldwide has been said to be his tutoring of Abel, both in school and privately. The two became friends and remained so until Abel's early death. Holmboe moved to the Royal Frederick University in 1826, where he worked until his own death in 1850.
  
  Holmboe's significant impact on mathematics in the fledgling Norway was his textbook in two volumes for secondary schools. It was widely used, but faced competition from Christopher Hansteen's alternative offering, sparking what may have been Norway's first debate about school textbooks. (Full article...)
• 

  

  In this graph, an even number of vertices (the four vertices numbered 2, 4, 5, and 6) have odd degrees. The sum of degrees of all six vertices is 2 + 3 + 2 + 3 + 3 + 1 = 14, twice the number of edges.

  
  In graph theory, the handshaking lemma is the statement that, in every finite undirected graph, the number of vertices that touch an odd number of edges is even. For example, if there is a party of people who shake hands, the number of people who shake an odd number of other people's hands is even. The handshaking lemma is a consequence of the degree sum formula, also sometimes called the handshaking lemma, according to which the sum of the degrees (the numbers of times each vertex is touched) equals twice the number of edges in the graph. Both results were proven by Leonhard Euler (1736) in his famous paper on the Seven Bridges of Königsberg that began the study of graph theory.
  
  Beyond the Seven Bridges of Königsberg Problem, which subsequently formalized Eulerian Tours, other applications of the degree sum formula include proofs of certain combinatorial structures. For example, in the proofs of Sperner's lemma and the mountain climbing problem the geometric properties of the formula commonly arise. The complexity class PPA encapsulates the difficulty of finding a second odd vertex, given one such vertex in a large implicitly-defined graph. (Full article...)
• 

  

  Example of a directed acyclic graph

  
  In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges (also called arcs), with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology (evolution, family trees, epidemiology) to information science (citation networks) to computation (scheduling).
  
  Directed acyclic graphs are also called acyclic directed graphs or acyclic digraphs. (Full article...)
• 
  
  

  

  

  Two symmetric orthographic projections

  
  In geometry, the complete or final stellation of the icosahedron is the outermost stellation of the icosahedron, and is "complete" and "final" because it includes all of the cells in the icosahedron's stellation diagram. That is, every three intersecting face planes of the icosahedral core intersect either on a vertex of this polyhedron or inside of it. It was studied by Max Brückner after the discovery of Kepler–Poinsot polyhedron. It can be viewed as an irregular, simple, and star polyhedron. (Full article...)
• 

  

  Hendrik Antoon Lorentz (right) after whom the Lorentz group is named and Albert Einstein whose special theory of relativity is the main source of application. Photo taken by Paul Ehrenfest 1921.

  
  
  The Lorentz group is a Lie group of symmetries of the spacetime of special relativity. This group can be realized as a collection of matrices, linear transformations, or unitary operators on some Hilbert space; it has a variety of representations. This group is significant because special relativity together with quantum mechanics are the two physical theories that are most thoroughly established, and the conjunction of these two theories is the study of the infinite-dimensional unitary representations of the Lorentz group. These have both historical importance in mainstream physics, as well as connections to more speculative present-day theories. (Full article...)
• 

  

  Graphical demonstration of the convergence of the sum 1/2 + 1/3 + 1/7 + 1/43 + ... to 1. Each row of k squares of side length 1/k has total area 1/k, and all the squares together exactly cover a larger square with area 1. Squares with side lengths 1/1807 or smaller are too small to see in the figure and are not shown.

  
  In number theory, Sylvester's sequence is an integer sequence in which each term is the product of the previous terms, plus one. Its first few terms are
  :2, 3, 7, 43, 1807, 3263443, 10650056950807, 113423713055421844361000443 (sequence A000058 in the OEIS).
  
  Sylvester's sequence is named after James Joseph Sylvester, who first investigated it in 1880. Its values grow doubly exponentially, and the sum of its reciprocals forms a series of unit fractions that converges to 1 more rapidly than any other series of unit fractions. The recurrence by which it is defined allows the numbers in the sequence to be factored more easily than other numbers of the same magnitude, but, due to the rapid growth of the sequence, complete prime factorizations are known only for a few of its terms. Values derived from this sequence have also been used to construct finite Egyptian fraction representations of 1, Sasakian Einstein manifolds, and hard instances for online algorithms. (Full article...)
• 
  Ronald Paul "Ron" Fedkiw (born February 27, 1968) is a full professor in the Stanford University department of computer science and a leading researcher in the field of computer graphics, focusing on topics relating to physically based simulation of natural phenomena and machine learning. His techniques have been employed in many motion pictures. He has earned recognition at the 80th Academy Awards and the 87th Academy Awards as well as from the National Academy of Sciences.
  
  His first Academy Award was awarded for developing techniques that enabled many technically sophisticated adaptations including the visual effects in 21st century movies in the Star Wars, Harry Potter, Terminator, and Pirates of the Caribbean franchises. Fedkiw has designed a platform that has been used to create many of the movie world's most advanced special effects since it was first used on the T-X character in Terminator 3: Rise of the Machines. His second Academy Award was awarded for computer graphics techniques for special effects for large scale destruction. Although he has won an Oscar for his work, he does not design the visual effects that use his technique. Instead, he has developed a system that other award-winning technicians and engineers have used to create visual effects for some of the world's most expensive and highest-grossing movies. (Full article...)
• 
  Fleiss' kappa (named after Joseph L. Fleiss) is a statistical measure for assessing the reliability of agreement between a fixed number of raters when assigning categorical ratings to a number of items or classifying items. This contrasts with other kappas such as Cohen's kappa, which only work when assessing the agreement between not more than two raters or the intra-rater reliability (for one appraiser versus themself). The measure calculates the degree of agreement in classification over that which would be expected by chance.
  
  Fleiss' kappa can be used with binary or nominal-scale. It can also be applied to ordinal data (ranked data): the MiniTab online documentation gives an example. However, this document notes: "When you have ordinal ratings, such as defect severity ratings on a scale of 1–5, Kendall's coefficients, which account for ordering, are usually more appropriate statistics to determine association than kappa alone." Keep in mind however, that Kendall rank coefficients are only appropriate for rank data. (Full article...)
• 

  

  A unit cube with a hole cut through it, large enough to allow Prince Rupert's cube to pass

  
  In geometry, Prince Rupert's cube is the largest cube that can pass through a hole cut through a unit cube without splitting it into separate pieces. Its side length is approximately 1.06, 6% larger than the side length 1 of the unit cube through which it passes. The problem of finding the largest square that lies entirely within a unit cube is closely related, and has the same solution.
  
  Prince Rupert's cube is named after Prince Rupert of the Rhine, who asked whether a cube could be passed through a hole made in another cube of the same size without splitting the cube into two pieces. A positive answer was given by John Wallis. Approximately 100 years later, Pieter Nieuwland found the largest possible cube that can pass through a hole in a unit cube. (Full article...)
• 
  Aderemi Oluyomi Kuku NNOM OON (20 March 1941 – 13 February 2022) was a Nigerian mathematician and academic, known for his contributions to the fields of algebraic K-theory and non-commutative geometry. Born in Ijebu-Ode, Ogun State, Nigeria, Kuku began his academic journey at Makerere University College and the University of Ibadan, where he earned his B.Sc. in Mathematics, followed by his M.Sc. and Ph.D. under Joshua Leslie and Hyman Bass. His doctoral research focused on the Whitehead group of p-adic integral group-rings of finite p-groups. Kuku held positions as a lecturer and professor at various Nigerian universities, including the University of Ife and the University of Ibadan, where he served as Head of the Department of Mathematics and Dean of the Postgraduate School. His research involved developing methods for computing higher K-theory of non-commutative rings and articulating higher algebraic K-theory in the language of Mackey functors. His work on equivariant higher algebraic K-theory and its generalisations impacted the field.
  
  During his career, Kuku was elected a Fellow of the African Academy of Sciences, the Nigerian Academy of Science, and the American Mathematical Society. He also received the Nigerian National Order of Merit and the Officer of the Order of the Niger. He served as president of the African Mathematical Union, where he worked to promote mathematics across Africa. Kuku's work extended beyond research, encompassing education and mentorship. He authored several books and articles, supervised graduate students, and fostered international collaborations. (Full article...)

Did you know (auto-generated) –

• ... that after Archimedes first defined convex curves, mathematicians lost interest in their analysis until the 19th century, more than two millennia later?
• ... that despite published scholarship to the contrary, Andrew Planta neither received a doctorate nor taught mathematics at Erlangen?
• ... that Fathimath Dheema Ali is the first Olympic qualifier from the Maldives?
• ... that in 1940 Xu Ruiyun became the first Chinese woman to receive a PhD in mathematics?
• ... that Fairleigh Dickinson's upset victory over Purdue was the biggest upset in terms of point spread in NCAA tournament history, with Purdue being a 23+1⁄2-point favorite?
• ... that more than 60 scientific papers authored by mathematician Paul Erdős were published posthumously?
• ... that mathematician Daniel Larsen was the youngest contributor to the New York Times crossword puzzle?
• ... that in the aftermath of the American Civil War, the only Black-led organization providing teachers to formerly enslaved people was the African Civilization Society?

More did you know –

Did you know...

• ...that it has not been proven whether or not every even integer greater than two can be expressed as the sum of two primes?
• ...that the sum of the first n odd numbers divided by the sum of the next n odd numbers is always equal to one third?
• ...that i to the power of i, where i is the square root of -1, is a real number?
• ...an infinite, nonrepeating decimal can be represented using only the number 1 using continued fractions?
• ...that 253931039382791 and the following 18 prime numbers all end in the digit 1?
• ...that the Electronic Frontier Foundation funds awards for the discovery of prime numbers beyond certain sizes?
• ...that pi can be computed using only the number 2 by the work of Viète?

Selected article –

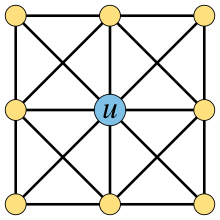
Image credit: User:Melchoir

The real number denoted by the recurring decimal 0.999… is exactly equal to 1. In other words, "0.999…" represents the same number as the symbol "1". Various proofs of this identity have been formulated with varying rigour, preferred development of the real numbers, background assumptions, historical context, and target audience.

The equality has long been taught in textbooks, and in the last few decades, researchers of mathematics education have studied the reception of this equation among students, who often reject the equality. The students' reasoning is typically based on one of a few common erroneous intuitions about the real numbers; for example, a belief that each unique decimal expansion must correspond to a unique number, an expectation that infinitesimal quantities should exist, that arithmetic may be broken, an inability to understand limits or simply the belief that 0.999… should have a last 9. These ideas are false with respect to the real numbers, which can be proven by explicitly constructing the reals from the rational numbers, and such constructions can also prove that 0.999… = 1 directly. (Full article...)

View all selected articles

Subcategories

Algebra | Arithmetic | Analysis | Complex analysis | Applied mathematics | Calculus | Category theory | Chaos theory | Combinatorics | Dynamical systems | Fractals | Game theory | Geometry | Algebraic geometry | Graph theory | Group theory | Linear algebra | Mathematical logic | Model theory | Multi-dimensional geometry | Number theory | Numerical analysis | Optimization | Order theory | Probability and statistics | Set theory | Statistics | Topology | Algebraic topology | Trigonometry | Linear programming

---

Mathematics | History of mathematics | Mathematicians | Awards | Education | Literature | Notation | Organizations | Theorems | Proofs | Unsolved problems

Full category tree. Select [►] to view subcategories.

Mathematics

Mathematics by country

Fields of mathematics

Mathematics-related lists

Mathematicians

Women in mathematics

Works about mathematics

Mathematics and art

Mathematical classification systems

Mathematical concepts

Mathematical constants

Mathematics and culture

Eponyms in mathematics

Mathematical examples

FL-Class Polyhedra articles

History of mathematics

Mathematics occupations

Mathematical notation

Outlines of mathematics and logic

Philosophy of mathematics

Mathematical projects

Mathematical proofs

Pseudomathematics

Set index articles on mathematics

Mathematical terminology

Mathematical theorems

Mathematical tools

Mathematics stubs

Topics in mathematics

General	Foundations	Number theory	Discrete mathematics
Mathematicians History of mathematics Philosophy of mathematics Mathematical notation Mathematical beauty Mathematics education Glossary of mathematical symbols	Foundations of mathematics Mathematical logic Proof theory Gödel's incompleteness theorems Model theory Recursion theory Set theory Naive set theory Axiomatic set theory Category theory Topos theory	Number theory Algebraic number theory Analytic number theory Arithmetic Fundamental theorem of arithmetic Numbers Natural numbers Prime numbers Rational numbers Algebraic numbers	Discrete mathematics Combinatorics Combinatorial geometry Coding theory Combinatorial design Enumerative combinatorics Combinatorial optimization Graph theory Order theory Lattice theory Digital Signal Processing Theoretical computer science Computability theory Complexity theory
Algebra	Analysis	Geometry and topology	Applied mathematics
Algebra Elementary algebra Abstract algebra Group theory Ring theory Field theory Commutative algebra Geometric algebra Linear algebra Matrix theory Multilinear algebra Universal algebra Fundamental theorem of algebra	Analysis Calculus Fundamental theorem of calculus Vector calculus Geometric calculus Measure theory Real analysis Complex analysis Differential equations Ordinary differential equations Partial differential equations Integral equations Approximation theory Special functions Potential theory Harmonic analysis Fourier analysis Functional analysis Operator theory	Geometry Euclidean geometry Trigonometry Analytic geometry Non-Euclidean geometry Affine geometry Projective geometry Convex geometry Discrete geometry Algebraic geometry Differential geometry K theory Gauge theory Riemannian geometry Lie groups Topology General topology Algebraic topology Geometric topology Differential topology	Applied mathematics Mathematical modeling Mathematical physics Dynamical systems Control theory Calculus of variations Optimization Mathematical economics Game theory Mathematical finance Statistics Probability theory Stochastic processes Numerical analysis Cryptography Information theory

Index of mathematics articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Related portals

WikiProjects

The Mathematics WikiProject is the center for mathematics-related editing on Wikipedia. Join the discussion on the project's talk page.

Project pages

• Participants
• Current activity
• Manual of style
• Conventions

Essays

• Advice on using Wikipedia for mathematics self-study
• Proofs

Subprojects

• PlanetMath Exchange (Talk)
• Graphics (Talk)
• Article assessment (Talk)

Related projects

Computer science | Cryptography | Game theory | Numbers | Physics | Science | Statistics

Things you can do

• Create a new article: List of requested articles
• Add a new image: Image requests
• Expand an article: Mathematics stubs
• Lend your expertise: Expert attention needed

In other Wikimedia projects

The following Wikimedia Foundation sister projects provide more on this subject:

• 

  Commons
  Free media repository

• 

  Wikibooks
  Free textbooks and manuals

• 

  Wikidata
  Free knowledge base

• 

  Wikinews
  Free-content news

• 

  Wikiquote
  Collection of quotations

• 

  Wikisource
  Free-content library

• 

  Wikiversity
  Free learning tools

• 

  Wiktionary
  Dictionary and thesaurus

More portals

Discover Wikipedia using portals

• 

  List of all portals

• 

  The arts portal

• 

  Biography portal

• 

  Current events portal

• 

  Geography portal

• 

  History portal

• 

  Mathematics portal

• 

  Science portal

• 

  Society portal

• 

  Technology portal

• 

  Random portal

• 

  WikiProject Portals