Logistic map

For the sigmoid curve, see Logistic function.

The behavior of the logistic map is shown in Cobweb plot form. The animation shows the change in behavior as the parameter (r in the figure) is increased from 1 to 4, starting from an initial value of 0.2.)

The logistic map is a discrete dynamical system defined by the quadratic difference equation:

$x_{n+1}=rx_{n}(1-x_{n}),$ (1)

Equivalently it is a recurrence relation and a polynomial mapping of degree 2. It is often referred to as an archetypal example of how complex, chaotic behaviour can arise from very simple nonlinear dynamical equations.

The map was initially utilized by Edward Lorenz in the 1960s to showcase properties of irregular solutions in climate systems. It was popularized in a 1976 paper by the biologist Robert May, in part as a discrete-time demographic model analogous to the logistic equation written down by Pierre François Verhulst. Other researchers who have contributed to the study of the logistic map include Stanisław Ulam, John von Neumann, Pekka Myrberg, Oleksandr Sharkovsky, Nicholas Metropolis, and Mitchell Feigenbaum.

Two simple examples

Dynamical Systems example

In the logistic map, r is a parameter, and x is a variable. It is a map in the sense that it maps a configuration or phase space to itself (in this simple case the space is one dimensional in the variable x), it can be interpreted as a tool to get next position in the configuration space after one time step. The difference equation is a discrete version of the logistic differential equation, which can be compared to a time evolution equation of the system.

Given an appropriate value for the parameter r and performing calculations starting from an initial condition $x_{0}$, you will obtain the sequence $x_{0}$, $x_{1}$, $x_{2}$, .... which can be interpreted as a sequence of time steps in the evolution of the system.

In the field of dynamical systems, this sequence is called an orbit, and the orbit changes depending on the value given to the parameter. When the parameter is changed, the orbit of the logistic map can change in various ways, such as settling on a single value, repeating several values periodically, or showing non-periodic fluctuations known as chaos.

Another way to understand this sequence is to apply recursively the logistic map (here represented by $f(x)$) to the initial state $x_{0}$

${\begin{aligned}x_{1}&=f(x_{0})\\x_{2}&=f(f(x_{0}))\\x_{3}&=f(f(f(x_{0})))\\\end{aligned}}$

Now this is important given this was the initial approach of Henri Poincaré to study dynamical systems and ultimately chaos starting from the study of fixed points or in other words states that do not change over time (i.e. when $x_{n}=...=x_{1}=x_{0}=f(x_{0})$). Many chaotic systems such as mandelbrot set are emerging from recursion of very simple quadratic non linear functions such as the logistic map.

Demographic model example

Taking the biological population model as an example x_n is a number between zero and one, which represents the ratio of existing population to the maximum possible population. This nonlinear difference equation is intended to capture two effects:

• reproduction, where the population will increase at a rate proportional to the current population when the population size is small,
• starvation (density-dependent mortality), where the growth rate will decrease at a rate proportional to the value obtained by taking the theoretical "carrying capacity" of the environment less the current population.

The usual values of interest for the parameter r are those in the interval [0, 4], so that x_n remains bounded on [0, 1]. The r = 4 case of the logistic map is a nonlinear transformation of both the bit-shift map and the μ = 2 case of the tent map. If r > 4, this leads to negative population sizes. (This problem does not appear in the older Ricker model, which also exhibits chaotic dynamics.) One can also consider values of r in the interval [−2, 0], so that x_n remains bounded on [−0.5, 1.5].

Characterization of the logistic map

The sequence behaviour from r=0.02 to r=4, one can visualize the horizontal coordinate as the time direction, and the vertical coordinate either as a position in space at time t or as the population size at time t

The animation shows the behaviour of the sequence $x_{n}$ over different values of the parameter r. A first interesting observation is that the sequence does not diverge and remains finite for r between 0 and 4. It is possible to see the following qualitative phenomena in order of time:

• exponential convergence to zero
• convergence to a fixed value
• initial oscillation and then convergence
• stable oscillations between two values
• growing oscillations between a set of values which is a multiples of two such as 2,4,8,16 etc.
• intermittence (i.e. sprouts of oscillations at the onset of chaos)
• fully developed chaotic oscillations
• topological mixing (i.e. the tendency of oscillations to cover the full available space).

The first 4 are avalilable also in standard linear systems, oscillations between two values are available too under resonance conditions. The other ones instead are peculiar to chaos. One shall compare these stages to the onset of turbulence which has strickingly similar phenomena. One shall also remember that chaos is not peculiar to non linearity only but that also infinite dimensional linear systems can exhibit chaos.

As mentioned above, the logistic map itself is an ordinary quadratic function, and even a junior high school student can calculate the trajectory . An important question in terms of dynamical systems is how the behavior of the trajectory changes when the parameter r is changed . Depending on the value of r, the behavior of the trajectory of the logistic map can be simple or complex . Below, we will explain how the behavior of the logistic map changes as r is increased.

Domain, graphs and fixed points

Graph of the logistic map ( the relationship between $x_{n+1}$ and $x_{n}$ ). The graph has the shape of a parabola, and the vertex of the parabola changes as the parameter r changes.

As mentioned above, the logistic map can be used as a model to consider the fluctuation of population size. In this case, the variable x of the logistic map is the number of individuals of an organism divided by the maximum population size, so the possible values of x are limited to 0 ≤ x ≤ 1. For this reason, the behavior of the logistic map is often discussed by limiting the range of the variable to the interval [0, 1].

If we try to restrict the variables to 0 ≤ x ≤ 1, then the range of the parameter r is necessarily restricted to 0 to 4 ( 0 ≤ r ≤ 4). This is because if $x_{n}$ is in the range [0, 1], then the maximum value of $x_{n+1}$ is r/4. Thus, when r > 4, the value of $x_{n+1}$ can exceed 1. On the other hand, when r is negative, x can take negative values.

A graph of the map can also be used to learn much about its behavior. The graph of the logistic map $x_{n+1}=rx(1-x_{n})$ is the plane curve that plots the relationship between $x_{n}$ and $x_{n+1}$, with $x_{n}$ (or x) on the horizontal axis and $x_{n+1}$ ( or f ( x ) ) on the vertical axis. The graph  of the logistic map looks like this, except for the case r = 0 :

It has the shape of a parabola with a vertex at

${\displaystyle (x_{n},x_{n+1})=\left(0.5,{\frac {r}{4}}\right)}$ (2-1)

When r is changed, the vertex moves up or down, and the shape of the parabola changes . In addition, the parabola of the logistic map intersects with the horizontal axis (the line where $x_{n+1}=0$) at two points . The two intersection points are $(x_{n},x_{n+1})=(0,0)$ and $(x_{n},x_{n+1})=(1,0)$, and the positions of these intersection points are constant and do not depend on the value of r.

An example of a spider web projection of a trajectory on the graph of the logistic map, and the locations of the fixed points $x_{f1}$ and $x_{f2}$ on the graph.

Graphs of maps, especially those of one variable such as the logistic map, are key to understanding the behavior of the map. One of the uses of graphs is to illustrate fixed points, called points. Draw a line y = x (a 45° line) on the graph of the map. If there is a point where this 45° line intersects with the graph, that point is a fixed point. In mathematical terms, a fixed point is

$f(x)=x$ (2-2)

It means a point that does not change when the map is applied. We will denote the fixed point as $x_{f}$. In the case of the logistic map, the fixed point that satisfies equation ( 2-2 ) is obtained by solving $rx(1-x)=x$.

${\displaystyle x_{f1}=0}$ (2-3)

$x_{f2}=1-{\frac {1}{r}}$ (2-4)

(except for r = 0). The concept of fixed points is of primary importance in discrete dynamical systems.

Another graphical technique that can be used for one-variable mappings is the spider web projection. After determining an initial value $x_{0}$ on the horizontal axis, draw a vertical line from the initial value $x_{0}$ to the curve of f(x). Draw a horizontal line from the  point where the curve of f(x) meets the 45° line of y = x, and then draw a vertical line from the point where the curve meets the 45° line to the curve of f(x). By repeating this process, a spider web or staircase-like diagram is created on the plane. This construction is in fact equivalent to calculating the trajectory graphically, and the spider web diagram created represents the trajectory starting from $x_{0}$. This projection allows the overall behavior of the trajectory to be seen at a glance.

Behavior dependent on r

The image below shows the amplitude and frequency content of a logistic map that iterates itself for parameter values ranging from 2 to 4. Again one can see initial linear behaviours then chaotic behaviour not only in the time domain (left) but especially in the frequency domain or spectrum (right), i.e. chaos is present at all scales as it is in the case of Energy cascade of Kolmogorov and it even propagates from one scale to another.

By varying the parameter r, the following behavior is observed:

Case when 0 ≤ r < 1

First, when the parameter r = 0, $x_{1}=0$, regardless of the initial value $x_{0}$. In other words, the trajectory of the logistic map when a = 0 is an trajectory in which all values after the initial value are 0, so there is not much to investigate in this case.

Next, when the parameter r is in the range 0 < r < 1, $x_{n}$ decreases monotonically for any value of $x_{0}$ between 0 and 1. That is, $x_{n}$ converges to 0 in the limit n → ∞. The point to which $x_{n}$ converges is the fixed point $x_{f1}$ shown in equation ( 2-3 ). Fixed points of  this type, where orbits around them converge, are called asymptotically stable, stable, or attractive. Conversely, if orbits around $x_{f}$ move away from $x_{f}$ as time n increases, the fixed point $x_{f}$ is called unstable or repulsive.

Spider plot (left) and time series ( n vs. x n ) (right) for parameter r = 0.9. The trajectory converges monotonically to 0.

A common and simple way to know whether a fixed point is asymptotically stable is to take the derivative of the map f. This derivative is expressed as $f'(x)$, $x_{f}$ is asymptotically stable if the following condition is satisfied .

$\left|f'(x_{f})\right|<1$ (3-1)

Tangent slopes of an asymptotically stable fixed point (left) and an unstable fixed point (right) and the state of the surrounding orbits

We can see this by graphing the map: if the slope of the tangent to the curve at $x_{f}$ is between −1 and 1, then $x_{f}$ is stable and the orbit around it is attracted to $x_{f}$. The derivative of the logistic map is

$f'(x)=r(1-2x)$ (3-2)

Therefore, for x = 0 and 0 < r < 1, 0 < f  '(0) < 1, so the fixed point $x_{f1}$ = 0  satisfies equation ( 3-1 ).

However, the discrimination method using equation ( 3-1 ) does not know the range of orbits from $x_{f}$ that are attracted to $x_{f}$. It only guarantees that x within a certain neighborhood of $x_{f}$ will converge. In this case, the domain of initial values that converge to 0 is the entire domain [0, 1], but to know this for certain, a separate study is required.

The method for determining whether a fixed point is unstable can be found by similarly differentiating the map. For r<1 if a fixed point $x_{f}$ is unstable if

$\left|f'(x_{f})\right|>1$ (3-3)

If the parameter lies in the range 0 < r < 1, then the other fixed point $x_{f2}=1-1/a$ is negative and therefore does not lie in the range [0, 1], but it does exist as an unstable fixed point .

Case when 1 ≤ r ≤ 2

In the general case with r between 1 and 2, the population will quickly approach the value ⁠r − 1/r⁠, independent of the initial population.

Transcritical bifurcation of the logistic map occurring at r = 1. For r < 1, $x_{f2}$ exists outside [0, 1] as an unstable fixed point, but for r = 1, the two fixed points collide, and for r > 1, $x_{f2}$ appears between [0, 1] as a stable fixed point.

When the parameter r = 1, the trajectory of the logistic map converges to 0 as before , but the convergence speed is slower at r = 1 . The fixed point 0 at r = 1 is asymptotically stable, but does not satisfy equation ( 3-1 ) . In fact, the discrimination method based on equation ( 3-1 ) works by approximating the map to the first order near the fixed point . When r = 1, this approximation does not hold, and stability or instability is determined by the quadratic (square) terms of the map, or in order words the second order perturbation.

When r = 1 is graphed, the curve is tangent to the 45° diagonal at x = 0. In this case, the fixed point $x_{f2}=1-1/r$, which exists in the negative range for $0<r<1$, is $x_{f2}=0$. For $x_{f2}=0$, that is, as r increases, the value of $x_{f2}$ approaches 0, and just at r = 1  , $x_{f2}$ collides with  $x_{f1}=0$. This collision gives rise to a phenomenon known as a transcritical bifurcation. Bifurcation is a term used to describe a qualitative change in the behavior of a dynamical system. In this case, transcritical bifurcation is when the stability of fixed points alternates between each other . That is, when r is less than 1, $x_{f1}$ is stable and $x_{f2}$ is unstable, but when r is greater than 1, $x_{f1}$ is unstable and $x_{f2}$ is stable. The parameter  values at which bifurcation occurs are called bifurcation points . In this case, r = 1 is the bifurcation point .

Fixed point $x_{f2}=1-1/r$ Example of monotonically decreasing convergence to ( r = 1.2, x 0 = 0.6)

Fixed point $x_{f2}=1-1/a$ Example of monotonically increasing convergence to ( r = 1.8, x 0 = 0.2)

As a result of the bifurcation, the orbit of the logistic map converges to the limit point $x_{f2}=1-1/r$ instead of $x_{f1}=0$. In particular, if the parameter $1<r\leq 2$, then the trajectory starting from a value $x_{0}$in the interval (0, 1), exclusive of 0 and 1, converges to $x_{f2}$ by increasing or decreasing monotonically . The difference in the convergence pattern depends on the range of the initial value. $0<x_{0}<1-1/r$

In the case of $1-1/r<x_{0}<1/r$ Then, it converges monotonically, $1/r<x_{0}<1$, the function converges monotonically except for the first step.

Furthermore, the fixed point $x_{f1}=0$ becomes unstable due to bifurcation, but continues to exist as a fixed point even after r > 1. This does not mean that there is no initial value other than $x_{f1}$ itself that  can reach this unstable fixed point  $x_{f1}$. This is $x_{0}=1$, and since the logistic map satisfies f ( 1) = 0 regardless of the value of r,  applying the map once to $x_{0}=1$ maps it to $x_{f1}=0$. A point such as x = 1 that can be reached directly as a fixed point by a  finite number of iterations of the map is called a final fixed point.

Case when 2 ≤ r ≤ 3

With r between 2 and 3, the population will also eventually approach the same value ⁠r − 1/r⁠, but first will fluctuate around that value for some time. The rate of convergence is linear, except for r = 3, when it is dramatically slow, less than linear (see Bifurcation memory).

When the parameter 2 < r < 3 , except for the initial values ​​0 and 1 , the fixed point $x_{f2}=1-1/r$ is the same as when 1 < r ≤ 2. However, in this case the convergence is not monotonically . As the variable approaches $x_{f2}$ , it becomes larger and smaller than $x_{f2}$ repeatedly, and follows a convergent trajectory that oscillates around $x_{f2}$.

. The value that is mapped to $x_{f2}$ by applying the mapping once is $f({\tilde {x}}_{f2})=x_{f2}$ -->

Animation of the spider projection at a = 2.8 , converging around a fixed point.

In general, bifurcation diagrams are useful for understanding bifurcations . These diagrams are graphs of fixed points (or periodic points , as described below ) x as a function of a parameter a , with a on the horizontal axis and x on the vertical axis. To distinguish between stable and unstable fixed points, the former curves are sometimes drawn as solid lines and the latter as dotted lines . When drawing a bifurcation diagram for the logistic map, we have a straight line representing the fixed point $x_{f1}=0$  and a straight line representing the fixed point $x_{f2}=1-1/a$ It can be seen that the curves representing a and b intersect at r = 1 , and that stability is switched between the two .

Bifurcation diagram of the logistic map for parameters 0 to 3. The blue line represents the fixed point $x_{f1}=0$, and the red line represents the fixed point $x_{f2}=1-1/r$ Represents.

Case when 3 ≤ r ≤ 3.44949

In the general case With r between 3 and 1 + √6 ≈ 3.44949 the population will approach permanent oscillations between two values. These two values are dependent on r and given by $x_{\pm }={\frac {1}{2r}}\left(r+1\pm {\sqrt {(r-3)(r+1)}}\right)$.

When the parameter is exactly r = 3 , the orbit also has a fixed point $x_{f2}=1-1/r$. However, the variables converge more slowly than when $2<r<3$. When $r=3$, the derivative $f'(x_{f2})$ reaches −1 and no longer satisfies equation (3-1). When r exceeds 3 , $f'(x_{f2})<-1$, and $x_{f2}$ becomes  an unstable fixed point. That is, another bifurcation occurs at $r=3$.

For $r=3$ a type of bifurcation known as a period doubling bifurcation occurs. For $r>3$ , the orbit no longer converges to a single point, but instead alternates between large and small values ​​even after a sufficient amount of time has passed. For example , for $r=3.3$, the variable alternates between the values ​​0.4794… and 0.8236… .

Spider diagram and time series for a = 3.3. The orbit is attracted to a stable 2-periodic point.

An orbit that cycles through the same values ​​periodically is called a periodic orbit . In this case, the final behavior of the variable as n → ∞ is a periodic orbit with two periods . Each value (point) that makes up a periodic orbit is called a periodic point . In the example where a = 3.3 , 0.4794… and 0.8236… are periodic points . If a certain x is a periodic point, then in the case of two periodic points, applying the map twice to x will return it to its original state, so

$f(f(x))=f^{2}(x)=x$ (3-4)

If we apply the logistic map equation (1-4) to this equation, we get

$r^{2}x(1-x)(1-ax(1-x))=x$ (3-5)

This gives us the following fourth-order equation . The solutions of this equation are the periodic points . In fact, there are two fixed points $x_{f1}=0$ and $x_{f2}=1-1/a$ also satisfies equation (3-4) . Therefore, of the solutions to equation (3-5), two correspond to $x_{f1}$ and $x_{f2}$, and the remaining two solutions are 2-periodic points . Let the 2-periodic points be denoted as $x_{f1}^{(2)}$ and $x_{f2}^{(2)}$, respectively. By solving equation (3-5), we can obtain them as follows

$x_{f1}^{(2)},\ x_{f2}^{(2)}={\frac {r+1\pm {\sqrt {(r+1)(r-3)}}}{2r}}$ (3-6)

A similar theory about the stability of fixed points can also be applied to periodic points. That is, a periodic point that attracts surrounding orbits is called an asymptotically stable periodic point, and a periodic point where the surrounding orbits move away is called an unstable periodic point . It is possible to determine the stability of periodic points in the same way as for fixed points . In the general case, consider $f^{k}(x)$ after k iterations of the map. Let $(f^{k})'(x)$ be the derivative  $df^{k}(x)/dx$ of the k-periodic point $x_{f}^{(k)}$. If $x_{f}^{(k)}$ satisfies :

$\left|(f^{k})'(x_{f}^{(k)})\right|<1$ (3-7)

then $x_{f}^{(k)}$ is asymptotically stable .

$\left|(f^{k})'(x_{f}^{(k)})\right|>1$ (3-8)

then $x_{f}^{(k)}$ is unstable .

The above discussion of the stability of periodic points can be easily understood by drawing a graph, just like the fixed points . In this diagram, the horizontal axis is xn and the vertical axis is $x_{n+2}$, and a curve is drawn that shows the relationship between $x_{n+2}$ and $x_{n}$. The intersections of this curve and the 45° line are points that satisfy equation (3-4), so the intersections represent fixed points and 2-periodic points. If we draw a graph of the logistic map $f^{2}(x)$, we can observe that the slope of the tangent at the fixed point $x_{f2}$ exceeds  1 at the boundary $r=3$ and becomes unstable. At the same time, two new intersections appear, which are the periodic points $x_{f1}^{(2)}$ and $x_{f2}^{(2)}$.

The relationship between $x_{n+2}$ and $x_{n}$ when r = 2.7 , before the period doubling bifurcation occurs. The orbit converges to a fixed point $x_{f2}$.

The relationship between $x_{n+2}$ and $x_{n}$ when r = 3. The tangent slope at the fixed point $x_{f2}$ is exactly 1, and a period doubling bifurcation occurs.

The relationship between $x_{n+2}$ and $x_{n}$ when r = 3.3 . $x_{f2}$ becomes unstable and the orbit converges to the periodic points $x_{f1}^{(2)}$ and $x_{f2}^{(2)}$.

When we actually calculate the differential coefficients of two periodic points for the logistic map, we get

$(f^{2})'(x_{f}^{(2)})=4+2r-r^{2}$ (3-9)

When this is applied to equation ( 3-7 ), the parameter a becomes :

$\left|4+2r-r^{2}\right|<1$ (3-10)

It can be seen that the 2-periodic points are asymptotically stable when this range is $3<r<1+{\sqrt {6}}$, i.e., when r exceeds $1+{\sqrt {6}}=3.44949...$ , the 2-periodic points are no longer asymptotically stable and their behavior changes .

Almost all initial values ​​in [0, 1] are attracted to the 2-periodic points, but $x_{f1}=0$ and $x_{f2}=1-1/a$ remains as an unstable fixed point in [0,1]. These unstable fixed points continue to remain in [0,1] even if r is increased . Therefore, when the initial value is exactly $x_{f1}$ or $x_{f2}$, the orbit  does not attract to a 2-periodic point . Moreover, when the initial value is the final fixed point for $x_{f1}$ or the final fixed point for $x_{f2}$, the orbit does not attract to a 2-periodic point . There are an infinite number of such final fixed points in [0, 1] . However, the number of such points is negligibly small compared to the set of real numbers [ 0, 1] .

Case when 3.44949 ≤ r ≤ 3.56995

With r between 3.44949 and 3.54409 (approximately), from almost all initial conditions the population will approach permanent oscillations among four values. The latter number is a root of a 12th degree polynomial (sequence A086181 in the OEIS).

With r increasing beyond 3.54409, from almost all initial conditions the population will approach oscillations among 8 values, then 16, 32, etc. The lengths of the parameter intervals that yield oscillations of a given length decrease rapidly; the ratio between the lengths of two successive bifurcation intervals approaches the Feigenbaum constant δ ≈ 4.66920. This behavior is an example of a period-doubling cascade.

When the parameter r exceeds $1+{\sqrt {6}}=3.44949...$, the previously stable 2-periodic points become unstable, stable 4-periodic points are generated, and the orbit gravitates toward a 4-periodic oscillation. That is, a period-doubling bifurcation occurs again at $r=3.44949...$. The value of x at the 4-periodic point is also

$f(f(f(f(x))))=f^{4}(x)=x$ (3-11)

satisfies, so that solving this equation allows the values ​​of x at the 4-periodic points to be found . However, equation (3-11) is a 16th-order equation, and even if we factor out the four solutions for the fixed points and the 2-periodic points, it is still a 12th-order equation . Therefore, it is no longer possible to solve this equation to obtain an explicit function of a that represents the values ​​of the 4-periodic points in the same way as for the 2-periodic points .

Examples of branching points up to 256 periods

The kth branch	Period 2k	Branch point ak
1	2	3.0000000
2	4	3.4494896
3	8	3.5440903
4	16	3.5644073
5	32	3.5687594
6	64	3.5696916
7	128	3.5698913
8	256	3.5699340

As a becomes larger, the stable 4-periodic point undergoes another period doubling, resulting in a stable 8-periodic point . As a increases, period doubling bifurcations occur infinitely: 16, 32, 64, ..., and so on, until an infinite period, i.e., an orbit that never returns to its original value . This infinite series of period doubling bifurcations is called a cascade . While these period doubling bifurcations occur infinitely, the intervals between a at which they occur decrease in a geometric progression. Thus, an infinite number of period doubling bifurcations occur before the parameter a reaches a finite value. Let the bifurcation from period 1 to period 2 that occurs at r = 3 be counted as the first period doubling bifurcation. Then, in this cascade of period doubling bifurcations, a stable 2k-periodic point occurs at the k-th bifurcation point. Let the k-th bifurcation point a be denoted as a k. In this case, it is known that $r_{k}$ converges to the following value as k → ∞ .

$r_{\infty }=\lim _{k\rightarrow \infty }r_{k}=3.56994...$ (3-12)

Furthermore, it is known that the rate of decrease of a k reaches a constant value in the limit, as shown in the following equation .

$\delta =\lim _{k\to \infty }{\frac {r_{k}-r_{k-1}}{r_{k+1}-r_{k}}}=4.66920...$ (3-13)

This value of δ is called the Feigenbaum constant because it was discovered by mathematical physicist Mitchell Feigenbaum. a∞ is called the Feigenbaum point. In the period doubling cascade, $f^{m}$  and $f^{2m}$ have the property that they are locally identical after an appropriate scaling transformation. The Feigenbaum constant can be found by a technique called renormalization that exploits this self-similarity. The properties that the logistic map exhibits in the period doubling cascade are also universal in a broader class of maps, as will be discussed later.  

To get an overview of the final behavior of an orbit for a certain parameter, an approximate bifurcation diagram, orbital diagram, is useful. In this diagram, the horizontal axis is the parameter r and the vertical axis is the variable x, as in the bifurcation diagram. Using a computer, the parameters are determined and, for example, 500 iterations are performed. Then, the first 100 results are ignored and only the results of the remaining 400 are plotted. This allows the initial transient behavior to be ignored and the asymptotic behavior of the orbit remains. For example, when one point is plotted for r , it is a fixed point, and when m points are plotted for r, it corresponds to an m-periodic orbit. When an orbital diagram is drawn for the logistic map, it is possible to see how the branch representing the stable periodic orbit splits, which represents a cascade of period-doubling bifurcations.

Bifurcation diagram of the period-doubling bifurcation cascade occurring between parameters $r_{1}=3$ and $a_{\infty }=3.56994...$. After 64 periods ($a_{5}$), the spacing becomes very narrow and almost collapses.

When the parameter $r=r_{\infty }$ is exactly the accumulation point of the period-doubling cascade, the variable $x_{n}$ is attracted to aperiodic orbits that never close. In other words, there exists a periodic point with infinite period at $r_{\infty }$. This aperiodic orbit is called the Feigenbaum attractor . The critical $2^{\infty }$ attractor. An attractor is a term used to refer to a region that has the property of attracting surrounding orbits, and is the orbit that is eventually drawn into and continues. The attractive fixed points and periodic points mentioned above are also members of the attractor family.

The structure of the Feigenbaum attractor is the same as that of a fractal figure called the Cantor set . The number of points that compose the Feigenbaum attractor is infinite and their cardinality is equal to the real numbers. However, no matter which two of the points are chosen, there is always an unstable periodic point between them, and the distribution of the points is not continuous . The fractal dimension of the Feigenbaum attractor, the Hausdorff dimension or capacity dimension , is known to be approximately 0.54.

An example of the construction of a Cantor set : if you keep removing the central third of a line segment infinitely, you will end up with a shape that appears to have zero length but has an uncountably infinite number of points , each of which has an infinitesimal neighborhood of other points.

Case when 3.56995 < r < 4

Evolution of different initial conditions as a function of r (The parameter k from the figure corresponds to the parameter r from the definition in the article.)

Evolution of different initial conditions as a function of r with bias (The parameter k from the figure corresponds to the parameter r from the definition in the article.)

• At r ≈ 3.56995 (sequence A098587 in the OEIS) is the onset of chaos, at the end of the period-doubling cascade. From almost all initial conditions, we no longer see oscillations of finite period. Slight variations in the initial population yield dramatically different results over time, a prime characteristic of chaos.
• This number shall be compared and understood as the equivalent of the Reynolds number for the onset of other chaotic phenomena such as turbulence and similar to the critical temperature of a phase transition. In essence the phase space contains a full subspace of cases with extra dynamical variables to characterize the microscopic state of the system, these can be understood as Eddies in the case of turbulence and order parameters in the case of phase transitions.
• Most values of r beyond 3.56995 exhibit chaotic behaviour, but there are still certain isolated ranges of r that show non-chaotic behavior; these are sometimes called islands of stability. For instance, beginning at 1 + √8 (approximately 3.82843) there is a range of parameters r that show oscillation among three values, and for slightly higher values of r oscillation among 6 values, then 12 etc.
• At $r=1+{\sqrt {8}}=3.8284...$, the stable period-3 cycle emerges.
• The development of the chaotic behavior of the logistic sequence as the parameter r varies from approximately 3.56995 to approximately 3.82843 is sometimes called the Pomeau–Manneville scenario, characterized by a periodic (laminar) phase interrupted by bursts of aperiodic behavior. Such a scenario has an application in semiconductor devices. There are other ranges that yield oscillation among 5 values etc.; all oscillation periods occur for some values of r. A period-doubling window with parameter c is a range of r-values consisting of a succession of subranges. The kth subrange contains the values of r for which there is a stable cycle (a cycle that attracts a set of initial points of unit measure) of period 2^kc. This sequence of sub-ranges is called a cascade of harmonics. In a sub-range with a stable cycle of period 2^k*c, there are unstable cycles of period 2^kc for all k < k*. The r value at the end of the infinite sequence of sub-ranges is called the point of accumulation of the cascade of harmonics. As r rises there is a succession of new windows with different c values. The first one is for c = 1; all subsequent windows involving odd c occur in decreasing order of c starting with arbitrarily large c.
• At $r=3.678...,x=0.728...$, two chaotic bands of the bifurcation diagram intersect in the first Misiurewicz point for the logistic map. It satisfies the equations $r^{3}-2r^{2}-4r-8=0,x=1-1/r$.
• Beyond r = 4, almost all initial values eventually leave the interval [0,1] and diverge. The set of initial conditions which remain within [0,1] form a Cantor set and the dynamics restricted to this Cantor set is chaotic.

For any value of r there is at most one stable cycle. If a stable cycle exists, it is globally stable, attracting almost all points. Some values of r with a stable cycle of some period have infinitely many unstable cycles of various periods.

The bifurcation diagram at right summarizes this. The horizontal axis shows the possible values of the parameter r while the vertical axis shows the set of values of x visited asymptotically from almost all initial conditions by the iterates of the logistic equation with that r value.

Bifurcation diagram for the logistic map. The attractor for any value of the parameter r is shown on the vertical line at that r.

The bifurcation diagram is a self-similar: if we zoom in on the above-mentioned value r ≈ 3.82843 and focus on one arm of the three, the situation nearby looks like a shrunk and slightly distorted version of the whole diagram. The same is true for all other non-chaotic points. This is an example of the deep and ubiquitous connection between chaos and fractals.

Magnification of the chaotic region of the map

Stable regions within the chaotic region, where a tangent bifurcation occurs at the boundary between the chaotic and periodic attractor, giving intermittent trajectories as described in the Pomeau–Manneville scenario

We can also consider negative values of r:

• For r between -2 and -1 the logistic sequence also features chaotic behavior.
• With r between -1 and 1 - √6 and for x₀ between 1/r and 1-1/r, the population will approach permanent oscillations between two values, as with the case of r between 3 and 1 + √6, and given by the same formula.

Chaos and the logistic map

A cobweb diagram of the logistic map, showing chaotic behaviour for most values of r > 3.57

Logistic function f (blue) and its iterated versions f², f³, f⁴ and f⁵ for r = 3.5. For example, for any initial value on the horizontal axis, f⁴ gives the value of the iterate four iterations later.

The relative simplicity of the logistic map makes it a widely used point of entry into a consideration of the concept of chaos. A rough description of chaos is that chaotic systems exhibits:

• Great Sensitivity on initial conditions: i.e. for a small or infinitesimal variation in the initial conditions you may have a large finite effect.
• Topologically transitive: i.e. the system tends to occupy all available states in a similar sense to fluid mixing.
• The system exhibits dense periodic orbits

These are properties of the logistic map for most values of r between about 3.57 and 4 (as noted above). A common source of such sensitivity to initial conditions is that the map represents a repeated folding and stretching of the space on which it is defined. In the case of the logistic map, the quadratic difference equation describing it may be thought of as a stretching-and-folding operation on the interval (0,1).

The following figure illustrates the stretching and folding over a sequence of iterates of the map. Figure (a), left, shows a two-dimensional Poincaré plot of the logistic map's state space for r = 4, and clearly shows the quadratic curve of the difference equation (1). However, we can embed the same sequence in a three-dimensional state space, in order to investigate the deeper structure of the map. Figure (b), right, demonstrates this, showing how initially nearby points begin to diverge, particularly in those regions of x_t corresponding to the steeper sections of the plot.

Two- and three-dimensional Poincaré plots show the stretching-and-folding structure of the logistic map

This stretching-and-folding does not just produce a gradual divergence of the sequences of iterates, but an exponential divergence (see Lyapunov exponents), evidenced also by the complexity and unpredictability of the chaotic logistic map. In fact, exponential divergence of sequences of iterates explains the connection between chaos and unpredictability: a small error in the supposed initial state of the system will tend to correspond to a large error later in its evolution. Hence, predictions about future states become progressively (indeed, exponentially) worse when there are even very small errors in our knowledge of the initial state. This quality of unpredictability and apparent randomness led the logistic map equation to be used as a pseudo-random number generator in early computers.

At r = 2, the function $rx(1-x)$ intersects $y=x$ precisely at the maximum point, so convergence to the equilibrium point is on the order of $\delta ^{2^{n}}$. Consequently, the equilibrium point is called "superstable". Its Lyapunov exponent is $-\infty$. A similar argument shows that there is a superstable $r$ value within each interval where the dynamical system has a stable cycle. This can be seen in the Lyapunov exponent plot as sharp dips.

Since the map is confined to an interval on the real number line, its dimension is less than or equal to unity. Numerical estimates yield a correlation dimension of 0.500±0.005 (Grassberger, 1983), a Hausdorff dimension of about 0.538 (Grassberger 1981), and an information dimension of approximately 0.5170976 (Grassberger 1983) for r ≈ 3.5699456 (onset of chaos). Note: It can be shown that the correlation dimension is certainly between 0.4926 and 0.5024.

It is often possible, however, to make precise and accurate statements about the likelihood of a future state in a chaotic system. If a (possibly chaotic) dynamical system has an attractor, then there exists a probability measure that gives the long-run proportion of time spent by the system in the various regions of the attractor. In the case of the logistic map with parameter r = 4 and an initial state in (0,1), the attractor is also the interval (0,1) and the probability measure corresponds to the beta distribution with parameters a = 0.5 and b = 0.5. Specifically, the invariant measure is

${\frac {1}{\pi {\sqrt {x(1-x)}}}}.$

Unpredictability is not randomness, but in some circumstances looks very much like it. Hence, and fortunately, even if we know very little about the initial state of the logistic map (or some other chaotic system), we can still say something about the distribution of states arbitrarily far into the future, and use this knowledge to inform decisions based on the state of the system.

Logistic map with Lyapunov exponent function

Graphical representation

The bifurcation diagram for the logistic map can be visualized with the following Python code:

import numpy as np
import matplotlib.pyplot as plt

interval = (2.8, 4)  # start, end
accuracy = 0.0001
reps = 600  # number of repetitions
numtoplot = 200
lims = np.zeros(reps)

fig, biax = plt.subplots()
fig.set_size_inches(16, 9)

lims[0] = np.random.rand()
for r in np.arange(interval[0], interval[1], accuracy):
    for i in range(reps - 1):
        lims[i + 1] = r * lims[i] * (1 - lims[i])

    biax.plot([r] * numtoplot, lims[reps - numtoplot :], "b.", markersize=0.02)

biax.set(xlabel="r", ylabel="x", title="logistic map")
plt.show()

Special cases of the map

Upper bound when 0 ≤ r ≤ 1

Although exact solutions to the recurrence relation are only available in a small number of cases, a closed-form upper bound on the logistic map is known when 0 ≤ r ≤ 1. There are two aspects of the behavior of the logistic map that should be captured by an upper bound in this regime: the asymptotic geometric decay with constant r, and the fast initial decay when x₀ is close to 1, driven by the (1 − x_n) term in the recurrence relation. The following bound captures both of these effects:

$\forall n\in \{0,1,\ldots \}\quad {\text{and}}\quad x_{0},r\in [0,1],\quad x_{n}\leq {\frac {x_{0}}{r^{-n}+x_{0}n}}.$

Solution when r = 4

The special case of r = 4 can in fact be solved exactly, as can the case with r = 2; however, the general case can only be predicted statistically. The solution when r = 4 is,

$x_{n}=\sin ^{2}\left(2^{n}\theta \pi \right),$

where the initial condition parameter θ is given by

$\theta ={\tfrac {1}{\pi }}\sin ^{-1}\left({\sqrt {x_{0}}}\right).$

For rational θ, after a finite number of iterations x_n maps into a periodic sequence. But almost all θ are irrational, and, for irrational θ, x_n never repeats itself – it is non-periodic. This solution equation clearly demonstrates the two key features of chaos – stretching and folding: the factor 2ⁿ shows the exponential growth of stretching, which results in sensitive dependence on initial conditions, while the squared sine function keeps x_n folded within the range [0,1].

For r = 4 an equivalent solution in terms of complex numbers instead of trigonometric functions is

$x_{n}={\frac {-\alpha ^{2^{n}}-\alpha ^{-2^{n}}+2}{4}}$

where α is either of the complex numbers

$\alpha =1-2x_{0}\pm {\sqrt {\left(1-2x_{0}\right)^{2}-1}}$

with modulus equal to 1. Just as the squared sine function in the trigonometric solution leads to neither shrinkage nor expansion of the set of points visited, in the latter solution this effect is accomplished by the unit modulus of α.

By contrast, the solution when r = 2 is

$x_{n}={\tfrac {1}{2}}-{\tfrac {1}{2}}\left(1-2x_{0}\right)^{2^{n}}$

for x₀ ∈ [0,1). Since (1 − 2x₀) ∈ (−1,1) for any value of x₀ other than the unstable fixed point 0, the term (1 − 2x₀)²ⁿ goes to 0 as n goes to infinity, so x_n goes to the stable fixed point ⁠1/2⁠.

Finding cycles of any length when r = 4

For the r = 4 case, from almost all initial conditions the iterate sequence is chaotic. Nevertheless, there exist an infinite number of initial conditions that lead to cycles, and indeed there exist cycles of length k for all integers k > 0. We can exploit the relationship of the logistic map to the dyadic transformation (also known as the bit-shift map) to find cycles of any length. If x follows the logistic map x_{n + 1} = 4x_n(1 − x_n) and y follows the dyadic transformation

$y_{n+1}={\begin{cases}2y_{n}&0\leq y_{n}<{\tfrac {1}{2}}\\2y_{n}-1&{\tfrac {1}{2}}\leq y_{n}<1,\end{cases}}$

then the two are related by a homeomorphism

$x_{n}=\sin ^{2}\left(2\pi y_{n}\right).$

The reason that the dyadic transformation is also called the bit-shift map is that when y is written in binary notation, the map moves the binary point one place to the right (and if the bit to the left of the binary point has become a "1", this "1" is changed to a "0"). A cycle of length 3, for example, occurs if an iterate has a 3-bit repeating sequence in its binary expansion (which is not also a one-bit repeating sequence): 001, 010, 100, 110, 101, or 011. The iterate 001001001... maps into 010010010..., which maps into 100100100..., which in turn maps into the original 001001001...; so this is a 3-cycle of the bit shift map. And the other three binary-expansion repeating sequences give the 3-cycle 110110110... → 101101101... → 011011011... → 110110110.... Either of these 3-cycles can be converted to fraction form: for example, the first-given 3-cycle can be written as ⁠1/7⁠ → ⁠2/7⁠ → ⁠4/7⁠ → ⁠1/7⁠. Using the above translation from the bit-shift map to the $r=4$ logistic map gives the corresponding logistic cycle 0.611260467... → 0.950484434... → 0.188255099... → 0.611260467.... We could similarly translate the other bit-shift 3-cycle into its corresponding logistic cycle. Likewise, cycles of any length k can be found in the bit-shift map and then translated into the corresponding logistic cycles.

However, since almost all numbers in [0,1) are irrational, almost all initial conditions of the bit-shift map lead to the non-periodicity of chaos. This is one way to see that the logistic r = 4 map is chaotic for almost all initial conditions.

The number of cycles of (minimal) length k = 1, 2, 3,… for the logistic map with r = 4 (tent map with μ = 2) is a known integer sequence (sequence A001037 in the OEIS): 2, 1, 2, 3, 6, 9, 18, 30, 56, 99, 186, 335, 630, 1161.... This tells us that the logistic map with r = 4 has 2 fixed points, 1 cycle of length 2, 2 cycles of length 3 and so on. This sequence takes a particularly simple form for prime k: 2 ⋅ ⁠2^{k − 1} − 1/k⁠. For example: 2 ⋅ ⁠2^{13 − 1} − 1/13⁠ = 630 is the number of cycles of length 13. Since this case of the logistic map is chaotic for almost all initial conditions, all of these finite-length cycles are unstable.

Universality

Period-doubling route to chaos

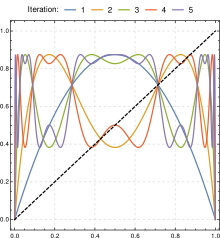
In the logistic map, we have a function $f_{r}(x)=rx(1-x)$, and we want to study what happens when we iterate the map many times. The map might fall into a fixed point, a fixed cycle, or chaos. When the map falls into a stable fixed cycle of length $n$, we would find that the graph of $f_{r}^{n}$ and the graph of $x\mapsto x$ intersects at $n$ points, and the slope of the graph of $f_{r}^{n}$ is bounded in $(-1,+1)$ at those intersections.

For example, when $r=3.0$, we have a single intersection, with slope bounded in $(-1,+1)$, indicating that it is a stable single fixed point.

As $r$ increases to beyond $r=3.0$, the intersection point splits to two, which is a period doubling. For example, when $r=3.4$, there are three intersection points, with the middle one unstable, and the two others stable.

As $r$ approaches $r=3.45$, another period-doubling occurs in the same way. The period-doublings occur more and more frequently, until at a certain $r\approx 3.56994567$, the period doublings become infinite, and the map becomes chaotic. This is the period-doubling route to chaos.

Relationship between $x_{n+2}$ and $x_{n}$ when $a=2.7$. Before the period doubling bifurcation occurs. The orbit converges to the fixed point $x_{f2}$.

Relationship between $x_{n+2}$ and $x_{n}$ when $a=3$. The tangent slope at the fixed point $x_{f2}$. is exactly 1, and a period doubling bifurcation occurs.

Relationship between $x_{n+2}$ and $x_{n}$ when $a=3.3$. The fixed point $x_{f2}$ becomes unstable, splitting into a periodic-2 stable cycle.

When $r=3.0$, we have a single intersection, with slope exactly $+1$, indicating that it is about to undergo a period-doubling.

When $r=3.4$, there are three intersection points, with the middle one unstable, and the two others stable.

When $r=3.45$, there are three intersection points, with the middle one unstable, and the two others having slope exactly $+1$, indicating that it is about to undergo another period-doubling.

When $r\approx 3.56994567$, there are infinitely many intersections, and we have arrived at chaos via the period-doubling route.

Scaling limit

Main article: Feigenbaum function

Approach to the scaling limit as $r$ approaches $r^{*}=3.5699\cdots$ from below.

At the point of chaos $r^{*}=3.5699\cdots$, as we repeat the period-doublings$f_{r^{*}}^{1},f_{r^{*}}^{2},f_{r^{*}}^{4},f_{r^{*}}^{8},f_{r^{*}}^{16},\dots$, the graphs seem to resemble each other, except that they are shrunken towards the middle, and rotated by 180 degrees, converging to a fractal.

Looking at the images, one can notice that at the point of chaos $r^{*}=3.5699\cdots$, the curve of $f_{r^{*}}^{\infty }$ looks like a fractal. Furthermore, as we repeat the period-doublings$f_{r^{*}}^{1},f_{r^{*}}^{2},f_{r^{*}}^{4},f_{r^{*}}^{8},f_{r^{*}}^{16},\dots$, the graphs seem to resemble each other, except that they are shrunken towards the middle, and rotated by 180 degrees.

This suggests to us a scaling limit: if we repeatedly double the function, then scale it up by $\alpha$ for a certain constant $\alpha$:$$f(x)\mapsto -\alpha f(f(-x/\alpha ))$$then at the limit, we would end up with a function $g$ that satisfies $g(x)=-\alpha g(g(-x/\alpha ))$. This is a Feigenbaum function, which appears in most period-doubling routes to chaos (thus it is an instance of universality). Further, as the period-doubling intervals become shorter and shorter, the ratio between two period-doubling intervals converges to a limit, the first Feigenbaum constant $\delta =4.6692016\cdots$.

For the wrong values of scaling factor $\alpha$, the map does not converge to a limit, but when $\alpha =2.5029\dots$, it converges.

At the point of chaos $r^{*}=3.5699\cdots$, as we repeat the functional equation iteration $f(x)\mapsto -\alpha f(f(-x/\alpha ))$ with $\alpha =2.5029\dots$, we find that the map does converge to a limit.

The constant $\alpha$ can be numerically found by trying many possible values. For the wrong values, the map does not converge to a limit, but when it is $\alpha =2.5029\dots$, it converges. This is the second Feigenbaum constant.

Chaotic regime

In the chaotic regime, $f_{r}^{\infty }$, the limit of the iterates of the map, becomes chaotic dark bands interspersed with non-chaotic bright bands.

In the chaotic regime, $f_{r}^{\infty }$, the limit of the iterates of the map, becomes chaotic dark bands interspersed with non-chaotic bright bands.

Other scaling limits

When $r$ approaches $r\approx 3.8494344$, we have another period-doubling approach to chaos, but this time with periods 3, 6, 12, ... This again has the same Feigenbaum constants $\delta ,\alpha$. The limit of ${\textstyle f(x)\mapsto -\alpha f(f(-x/\alpha ))}$ is also the same Feigenbaum function. This is an example of universality.

Logistic map approaching the period-doubling chaos scaling limit $r^{*}=3.84943\dots$ from below. At the limit, this has the same shape as that of $r^{*}=3.5699\cdots$, since all period-doubling routes to chaos are the same (universality).

We can also consider period-tripling route to chaos by picking a sequence of $r_{1},r_{2},\dots$ such that $r_{n}$ is the lowest value in the period-$3^{n}$ window of the bifurcation diagram. For example, we have $r_{1}=3.8284,r_{2}=3.85361,\dots$, with the limit $r_{\infty }=3.854077963\dots$. This has a different pair of Feigenbaum constants $\delta =55.26\dots ,\alpha =9.277\dots$. And $f_{r}^{\infty }$converges to the fixed point to $$f(x)\mapsto -\alpha f(f(f(-x/\alpha )))$$As another example, period-4-pling has a pair of Feigenbaum constants distinct from that of period-doubling, even though period-4-pling is reached by two period-doublings. In detail, define $r_{1},r_{2},\dots$ such that $r_{n}$ is the lowest value in the period-$4^{n}$ window of the bifurcation diagram. Then we have $r_{1}=3.960102,r_{2}=3.9615554,\dots$, with the limit $r_{\infty }=3.96155658717\dots$. This has a different pair of Feigenbaum constants $\delta =981.6\dots ,\alpha =38.82\dots$.

In general, each period-multiplying route to chaos has its own pair of Feigenbaum constants. In fact, there are typically more than one. For example, for period-7-pling, there are at least 9 different pairs of Feigenbaum constants.

Generally, ${\textstyle 3\delta \approx 2\alpha ^{2}}$, and the relation becomes exact as both numbers increase to infinity: $\lim \delta /\alpha ^{2}=2/3$.

Feigenbaum universality of 1-D maps

Universality of one-dimensional maps with parabolic maxima and Feigenbaum constants $\delta =4.669201...$, $\alpha =2.502907...$.

The gradual increase of $G$ at interval $[0,\infty )$ changes dynamics from regular to chaotic one with qualitatively the same bifurcation diagram as those for logistic map.

Renormalization estimate

The Feigenbaum constants can be estimated by a renormalization argument. (Section 10.7,).

By universality, we can use another family of functions that also undergoes repeated period-doubling on its route to chaos, and even though it is not exactly the logistic map, it would still yield the same Feigenbaum constants.

Define the family $$f_{r}(x)=-(1+r)x+x^{2}$$The family has an equilibrium point at zero, and as $r$ increases, it undergoes period-doubling bifurcation at $r=r_{0},r_{1},r_{2},...$.

The first bifurcation occurs at $r=r_{0}=0$. After the period-doubling bifurcation, we can solve for the period-2 stable orbit by $f_{r}(p)=q,f_{r}(q)=p$, which yields $${\begin{cases}p={\frac {1}{2}}(r+{\sqrt {r(r+4)}})\\q={\frac {1}{2}}(r-{\sqrt {r(r+4)}})\end{cases}}$$At some point $r=r_{1}$, the period-2 stable orbit undergoes period-doubling bifurcation again, yielding a period-4 stable orbit. In order to find out what the stable orbit is like, we "zoom in" around the region of $x=p$, using the affine transform $T(x)=x/c+p$. Now, by routine algebra, we have$$(T^{-1}\circ f_{r}^{2}\circ T)(x)=-(1+S(r))x+x^{2}+O(x^{3})$$where $S(r)=r^{2}+4r-2,c=r^{2}+4r-3{\sqrt {r(r+4)}}$. At approximately $S(r)=0$, the second bifurcation occurs, thus $S(r_{1})\approx 0$.

By self-similarity, the third bifurcation when $S(r)\approx r_{1}$, and so on. Thus we have $r_{n}\approx S(r_{n+1})$, or $r_{n+1}\approx {\sqrt {r_{n}+6}}-2$. Iterating this map, we find $r_{\infty }=\lim _{n}r_{n}\approx \lim _{n}S^{-n}(0)={\frac {1}{2}}({\sqrt {17}}-3)$, and $\lim _{n}{\frac {r_{\infty }-r_{n}}{r_{\infty }-r_{n+1}}}\approx S'(r_{\infty })\approx 1+{\sqrt {17}}$.

Thus, we have the estimates $\delta \approx 1+{\sqrt {17}}=5.12...$, and $\alpha \approx r_{\infty }^{2}+4r_{\infty }-3{\sqrt {r_{\infty }^{2}+4r_{\infty }}}\approx -2.24...$. These are within 10% of the true values.

Relation to logistic ordinary differential equation

The logistic map exhibits numerous characteristics of both periodic and chaotic solutions, whereas the logistic ordinary differential equation (ODE) exhibits regular solutions, commonly referred to as the S-shaped sigmoid function. The logistic map can be seen as the discrete counterpart of the logistic ODE, and their correlation has been extensively discussed in literature

Occurrences and similar systems

• In a toy model for discrete laser dynamics:

$x\rightarrow Gx(1-\tanh(x))$, where $x$ stands for electric field amplitude, $G$ is laser gain as bifurcation parameter.

• Hofstadter sequences are an example of one dimensional quasi-random, aperiodic, chaotic sequences again defined by recursion, a very special case is the logistic map
• Hofstadter butterfly is a two dimensional example of the emergence of chaos starting from the combination of two periodic phenomena (magnetic field and crystal spacing) with two different periods that divided by each other are an irrational number

See also

• Logistic function, solution of the logistic map's continuous counterpart: the Logistic differential equation.
• Lyapunov stability#Definition for discrete-time systems
• Malthusian growth model
• Periodic points of complex quadratic mappings, of which the logistic map is a special case confined to the real line
• Radial basis function network, which illustrates the inverse problem for the logistic map.
• Schröder's equation
• Stiff equation

References

• Thompson, JMT; Stewart, HB (2002). Nonlinear Dynamics and Chaos (2nd ed.). Wiley.
• Devaney, Robert L. (1989). An introduction to Chaotic Dynamical systems (2nd ed.). Addison-Wesley.
• Hirsch; Smale; Devaney (2007). Differential Equations, Dynamical systems, and an introduction to chaos.
• Gulick, Denny (1995). "Encounter with Chaos: A Mathematical Approach to Dynamical Systems". ISBN 4-7828-1009-1.
• Grassberger, P.; Procaccia, I. (1983). "Measuring the strangeness of strange attractors". Physica D. 9 (1–2): 189–208. Bibcode:1983PhyD....9..189G. doi:10.1016/0167-2789(83)90298-1.
• Grassberger, P. (1981). "On the Hausdorff dimension of fractal attractors". Journal of Statistical Physics. 26 (1): 173–179. Bibcode:1981JSP....26..173G. doi:10.1007/BF01106792. S2CID 119833080.
• Sprott, Julien Clinton (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 978-0-19-850840-3.
• Strogatz, Steven (2000). Nonlinear Dynamics and Chaos. Perseus Publishing. ISBN 978-0-7382-0453-6.
• Strogatz, Steven (2015). Nonlinear Dynamics and Chaos With Applications to Physics, Biology, Chemistry, and Engineering. CRC press. ISBN 978-0-8133-4910-7.
• Tufillaro, Nicholas; Abbott, Tyler; Reilly, Jeremiah (1992). An Experimental Approach to Nonlinear Dynamics and Chaos. Addison-Wesley New York. ISBN 978-0-201-55441-0.

External links

• The Chaos Hypertextbook. An introductory primer on chaos and fractals.
• An interactive visualization of the logistic map as a Jupyter notebook
• The Logistic Map and Chaos by Elmer G. Wiens
• Complexity & Chaos (audiobook) by Roger White. Chapter 5 covers the Logistic Equation.
• "History of iterated maps," in A New Kind of Science by Stephen Wolfram. Champaign, IL: Wolfram Media, p. 918, 2002.
• "A very brief history of universality in period doubling" by P. Cvitanović
• "A not so short history of Universal Function" by P. Cvitanović
• Discrete Logistic Equation by Marek Bodnar after work by Phil Ramsden, Wolfram Demonstrations Project.
• Multiplicative coupling of 2 logistic maps by C. Pellicer-Lostao and R. Lopez-Ruiz after work by Ed Pegg Jr, Wolfram Demonstrations Project.
• Using SAGE to investigate the discrete logistic equation